空间算子是预报方程中最关键的部分,需要对它们非常熟悉,了解它们的性质。
基础算子
- 水平梯度算子 ∇f
- 水平散度算子 ∇⋅F
- 水平旋度算子 ∇×F
- 水平通量算子 ∇⋅(fv)
- 水平平流算子 v⋅∇f
算子之间的关系(通过内积定义)
(∇⋅F,g)=−(F,∇g)(∇×F,g)=−(F,∇⊥g)
球面坐标系形式
球坐标系下的矢量在计算导数时存在一定问题,因为球坐标基矢量随坐标变化,所以矢量的空间变化包含了基矢量的变化。下面列出的是各个算子的微分形式:
∇f=acosφ1∂λ∂fiλ+a1∂φ∂fiφ
∇⋅F=acosφ1(∂λ∂Fλ+∂φ∂Fφcosφ)
∇×F=acosφ1(∂λ∂Fφ−∂φ∂Fλcosφ)
∇⋅(vf)=acosφ1(∂λ∂fu+∂φ∂fvcosφ)
v⋅∇f=acosφu∂λ∂f+av∂φ∂f
积分形式更容易操作
[∇×v]A:=∣A∣→0lim∣A∣1∫∂Av⋅dl
[∇⋅(vf)]A:=∣A∣→0lim∣A∣1∫∂Afu⋅nds
其中dl是沿着二维区域A边界的线段矢量,ds是沿区域A边界的面元,n是ds的法向量,指向区域A外侧,∣A∣是区域面积或体积。
离散方法
经纬网格
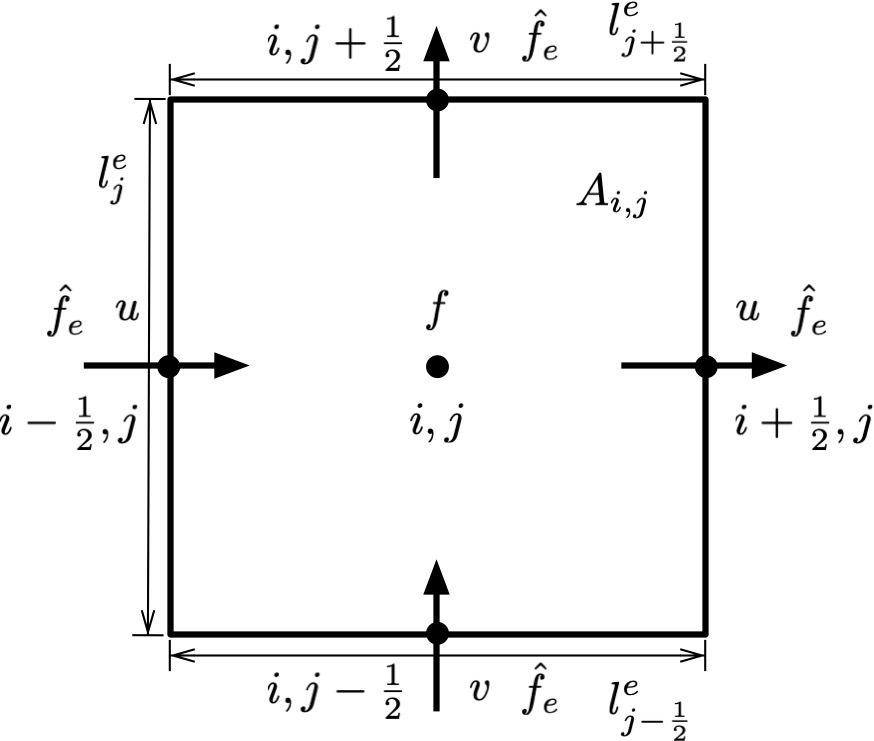 [∇⋅(vf)]i,j=Aj1[(leuf^e)i+21,j−(leuf^e)i−21,j+(levf^e)i,j+21−(levf^e)i,j−21]
[∇⋅(vf)]i,j=Aj1[(leuf^e)i+21,j−(leuf^e)i−21,j+(levf^e)i,j+21−(levf^e)i,j−21]